ncert solutions for class 10 maths surface area and volume exercise 13.5 fully cover

Table of Contents

ncert solutions for class 10 maths surface area and volume exercise 13.5

बिहार बोर्ड इंटर/Matric परीक्षा 2022 के सभी विद्यार्थी के सभी विषय की सभी प्रकार के प्रश्न का प्रारूप और PDF वर्ग नोट विषयवार सभी प्रकार के study note ( MCQ , Short question long question ) Bharti Bhawan

Bihar Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5

BSEB Bihar Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5

Bihar Board Class 10 Maths पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5

प्रश्न 1.
व्यास 3 mm वाले ताँबे के तार को 12 cm लम्बे और 10 cm व्यास वाले एक बेलन पर इस प्रकार लपेटा जाता है कि वह बेलन के व्रक पृष्ठ को पूर्णतया ढक लेता है। तार की लम्बाई और द्रव्यमान ज्ञात कीजिए, यह मानते हुए कि ताँबे का द्रव्यमान 8.88 g/cm³ हैं।
हल
बेलन का व्यास = 10 cm तथा बेलन की ऊँचाई = 12 cm
बेलन की परिधि = π × व्यास = π × 10 = 10π cm
बेलन पर 1 चक्कर लपेटने के लिए तार की लम्बाई = 10π cm
जब बेलन पर तार का 1 चक्कर लपेटते हैं तो उसकी 3 mm लम्बाई ढक जाती है।
जब बेलन पर तार के 2 चक्कर लपेटते हैं तो उसकी (2 × 3) mm लम्बाई ढक जाती है।
जब बेलन पर तार के 3 चक्कर लपेटते हैं तो उसकी (3 × 3) mm लम्बाई ढक जाती है।
जब बेलन पर तार के 4 चक्कर लपेटते हैं तो उसकी (4 × 3) mm लम्बाई ढक जाती है।
तब, सम्पूर्ण बेलन को ढकने के लिए तार के 1203 = 40 चक्कर लपेटने होंगे।
40 चक्कर बेलन पर लपेटने के लिए आवश्यक तार की माप
= 40 × 10π
= 400π cm
= 400 × 3.14 cm
= 1256 cm
= 12.56 m (लगभग)
अत: तार की अभीष्ट लम्बाई = 12.56 m
तथा तार का द्रव्यमान = 1256 × 8.88 g
= 11153.3 g
= 11.153 kg

प्रश्न 2.
एक समकोण त्रिभुज, जिसकी भुजाएँ 3 cm और 4 cm हैं (कर्ण के अतिरिक्त), को उसके कर्ण के परितः घुमाया जाता है। इस प्रकार प्राप्त द्वि-शंकु (double cone) के आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (r का मान जो भी उपयुक्त लगे, प्रयोग कीजिए।)
हल

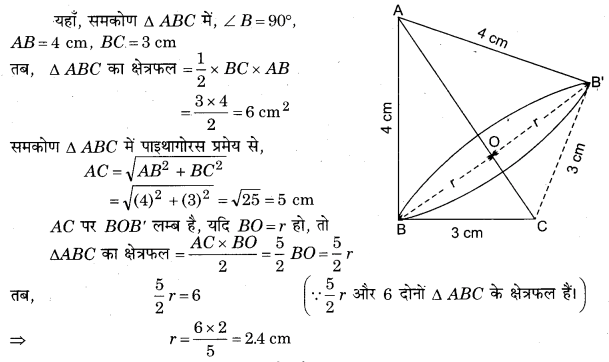
ncert solutions for class 10 maths surface area and volume exercise 13.5

अतः समकोण ∆ABC के परिक्रमण से बने द्वि-शंकु की त्रिज्या (r) = 2.4 cm
तब, द्वि-शंकु (दोनों शंकुओं) का आयतन = शंकु (ABB’) का आयतन + शंकु (CBB’) का आयतन

= $\frac{1}{3}\pi r^2$ (AO) + $\frac{1}{3}\pi r^2$ (OC)

= $\frac{1}{3}\pi r^2$ (AO + OC)
= $\frac{1}{3}\pi r^2$ (AC) (∵ AO + OC = AC)
= $\frac{1}{3}\pi$ × (2.4)² × 5
= 9.6π
= 9.6 × 3.14
= 30.144 cm³
और द्वि-शंकु (दोनों शंकुओं) का पृष्ठीय क्षेत्रफल = शंकु (ABB’) का वक्रपृष्ठ + शंकु (CBB’) का वक्र पृष्ठ
= πr(AB) + πr(BC)
= πr(AB + BC)
= 3.14 × 2.4 × (4 + 3)
= 3.14 × 2.4 × 7
= 52.75 cm²
अतः द्वि-शंकु का आयतन = 30.144 cm³
तथा पृष्ठीय क्षेत्रफल = 52.75 cm² (लगभग)।

प्रश्न 3.
एक टंकी, जिसके आन्तरिक मापन 150 cm × 120 cm × 110 cm हैं, में 129600 cm³ पानी है। इस पानी में कुछ छिद्र वाली ईंटें तब तक डाली जाती हैं, जब तक कि टंकी पूरी ऊपर तक भर न जाए। प्रत्येक ईंट अपने आयतन का 117 पानी सोख लेती है। यदि प्रत्येक ईंट की माप 22.5 cm × 7.5 cm × 6.5 cm है तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं, ताकि उसमें से पानी बाहर न बहे?
हल
टंकी का आयतन = 150 × 120 × 110 cm³ = 1980000 cm³
टंकी में भरे पानी का आयतन = 129600 cm³
प्रत्येक ईंट का आयतन = 22.5 × 7.5 × 6.5 cm³ = 1096.875 cm³
माना टंकी में x ईंटें डालने पर टंकी पानी से ऊपर तक भर जाएगी।
तब, x ईंटों का आयतन = 1096.875x cm³

Q3 1

प्रश्न 4.
किसी महीने के 15 दिनों में, एक नदी की घाटी में 10 cm वर्षा हुई। यदि इस घाटी का क्षेत्रफल 97280 km² है तो दर्शाइए कि कल वर्षा लगभग तीन नदियों के सामान्य पानी के योग के समतुल्य थी, जबकि प्रत्येक नदी 1072 km लम्बी, 75 m चौड़ी और 3 m गहरी है।
हल
प्रत्येक नदी का आयतन = 1072 km × 75 m × 3 m
= 1072 × 75 × 3 × 1000 m³
= 241200000 m³
तीनों नदियों के कुल पानी का आयतन = 3 × 241200000 m³
नदियों का कुल पानी = 723600000 m³
घाटी का क्षेत्रफल = 97280 km²
= 97280 × (1000)² m²
= 97280000000 m²
वर्षा के पानी का आयतन = 97280000000 × $\frac{10}{100}$ m³ (∵ 10 cm = $\frac{10}{100}$ m)
= 9728000000 m³
ये दोनों आयतन बराबर होने चाहिए लेकिन ये बराबर नहीं हैं।
इससे स्पष्ट है कि प्रश्न में दिए तथ्य असंगत हैं।

प्रश्न 5.
टीन की बनी हुई एक तेल की कुप्पी 10 cm लम्बे एक बेलन में एक शंकु के छिन्नक को जोड़ने से बनी है। यदि इसकी कुल ऊँचाई 22 cm है, बेलनाकार भाग का व्यास 8 cm है और कुप्पी के ऊपरी सिरे का व्यास 18 cm है, तो इसके बनाने में लगी टीन की चादर का क्षेत्रफल ज्ञात कीजिए।

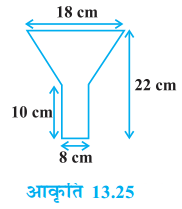
Bihar Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5 Q5

हल
दिया है, बेलनाकार भाग की ऊँचाई (h) = 10 cm
कुप्पी की कुल ऊँचाई = 22 cm
शंकु के छिन्नक की ऊँचाई (H) = 22 – 10 = 12 cm
शंकु के छिन्नक की ऊपरी त्रिज्या (R₁) = $\frac{18}{2}$ = 9 cm
शंकु के छिन्नक की निचली त्रिज्या (R₂) = $\frac{8}{2}$ = 4 cm
बेलनाकार भाग की त्रिज्या (r) = 4 cm
बेलनाकार भाग का वक्रपृष्ठ = 2πrh
= 2π × 4 × 10
= 80π cm²
शंकु के छिन्नक की तिर्यक ऊँचाई
Q3 1 1
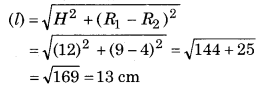
शंकु के छिन्नक का वक्र पृष्ठ = π(R₁ + R₂)l
= π(9 + 4) × 13
= 169π cm²
अतः कुप्पी का कुल पृष्ठीय क्षेत्रफल = बेलनाकार भाग का वक्र पृष्ठ + शंकु छिन्नक का वक्र पृष्ठ
= 80π + 169π
= 249π cm²
= 249 × 227 cm²
= 54787 cm²
= 78247 cm²
अत: कुप्पी को बनाने में लगी टीन की चादर का क्षेत्रफल = 78247 cm²

प्रश्न 6.
शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, वक्र पृष्ठीय क्षेत्रफल और सम्पूर्ण पृष्ठीय क्षेत्रफल के सूत्रों को सिद्ध कीजिए।
हल
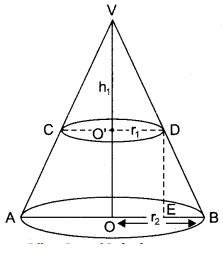
Bihar Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5 Q6
माना एक शंकु (VAB) का शीर्ष V, आधार की त्रिज्या r₂ और तिर्यक ऊँचाई l₂ है। इस शंकु के शीर्ष V से h₁ नीचे स्थित बिन्दु O’ से आधार के समान्तर एक शंकु (VCD) काटा गया है जिसकी त्रिज्या r₁ तथा तिर्यक ऊँचाई l₁ है।
बिन्दु D से आधार पर लम्ब DE खींचा।
ΔVOD तथा ΔDOB में,
∠VO’D = ∠DEB [∵ VO ⊥ AB और VO’ ⊥ CD] ∠VDO’ = ∠DBE [संगत कोण] ΔVOD और ΔDEB समरूप हैं।
Bihar Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5 Q6.1
छिन्नक का वक्र पृष्ठीय क्षेत्रफल = शंकु (VAB) का वक्र पृष्ठ – शंकु (VCD) का वक्र पृष्ठ

Q 6

प्रश्न 7.
शंकु के एक छिन्नक के लिए, स्पष्ट संकेतों का प्रयोग करते हुए, आयतन का सूत्र सिद्ध कीजिए।
हल

पिछले प्रश्न से, शंकु (VAB) की ऊँचाई h₂ तथा त्रिज्या r₂ है।

Bihar Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5 Q7.1

ncert solutions for class 10 maths surface area and volume

ncert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volume ncert solutions for class 10 maths surface area and volume ncert solutions for class 10 maths surface area and volume ncert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volume
ncert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volume ncert solutions for class 10 maths surface area and volume ncert solutions for class 10 maths surface area and volume ncert solutions for class 10 maths surface area and volumencert solutions for class 10 maths surface area and volume

ncert solutions for class 10 maths surface area and volume exercise 13.5

Bihar Board Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5

Leave a Reply Cancel reply