NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi
एनसीईआरटी कक्षा 10 गणित अध्याय 5: समांतर श्रेढियाँ प्रश्नावली 5.4 समाधान हिंदी में: क्या आप कक्षा 10 के गणित के एनसीईआरटी समाधान हिंदी में खोज रहे हैं, यदि हाँ तो आप सही जगह पर आए हैं? हमारे विशेषज्ञ ने सभी विषयों के लिए एनसीईआरटी कक्षा 10 के समाधान बहुत ही वर्णनात्मक तरीके से बनाए हैं ताकि कोई भी छात्र इसे आसानी से समझ सके। हिंदी में यह समाधान सभी छात्रों के लिए बहुत मददगार होने वाला है। हमने सभी विषयों के एनसीईआरटी कक्षा 10 के नोट्स भी बहुत ही सरल तरीकों से हिंदी में बनाए हैं।
![]()
अध्याय 5: समांतर श्रेढियाँ प्रश्नावली 5.4
1.A.P. : 121, 117, 113 ………… का कौन-सा पद सबसे पहला ऋणात्मक पद होगा?
हल:
दिया गया सूची है: 121, 117, 113, . . .
पहला पद, a = 121
सार्व अंतर, d = 117 – 121 = – 4
माना, an पहला ऋणात्मक पद होगा।
an < 0
an = a + (n − 1)d < 0
⇒ 121 + (n − 1)( – 4) < 0
⇒ 121 – 4n + 4 < 0
⇒ 125 – 4n < 0
⇒ 125 < 4n
⇒ 4n > 125
⇒ n > \(\frac {125}4\)
⇒ n > 31.25
⇒ n = 32
अत:, 32वाँ पद पहला ऋणात्मक पद होगा। (उत्तर)
2. किसी AP के तीसरे और सातवें पदों का योग 6 है और उनका गुणनफल 8 है। इस AP के प्रथम 16 पदों का योग ज्ञात कीजिए।
हल:
दिया गया है,
a3 + a7 = 6 ……………………….(i)
तथा
a3 × a7 = 8 ……………………..(ii)
हम जानते हैं कि,
an = a + (n − 1)d
a3 = a + (3 – 1)d
a3 = a + 2d ………………………(iii)
a7 = a + (7 – 1)d
a7 = a + 6d ………………………..(iv)
समीकरण (iii) तथा (iv) का मान समीकरण (i) में रखने पर,
a + 2d + a + 6d = 6
2a + 8d = 6
a + 4d=3
a = 3 – 4d ……………………(v)
समीकरण (iii) तथा (iv) का मान समीकरण (ii) में रखने पर,
(a + 2d)×(a + 6d) = 8
समीकरण (v) से a का मान रखने पर,
(3 – 4d + 2d) × (3 – 4d + 6d) = 8
⇒ (3 – 2d) × (3 + 2d) = 8
⇒ 32 – (2d)2 = 8
⇒ 9 – 4d2 = 8
⇒ – 4d2 = 8 – 9
⇒ 4d2 = 1
⇒ d2 = \(\frac 14\)
⇒ d = \(\sqrt{\frac{1}{4}}\)
⇒ d = \(\pm \frac{1}{2}\)
⇒ d = \(\frac 12\) or, d = \(-\;\frac 12\)
d का मान समीकरण (v) में रखने पर,
If d = \(\frac 12\)
a = 3 – 4d = 3 – 4 × \(\frac 12\) = 3 – 2 = 1
If d = \(-\;\frac 12\)
a = 3 – 4d = 3 – 4 × \(-\;\frac 12\) = 3 + 2 = 5
हम जानते हैं कि,
प्रथम n पदों का योग, Sn = \(\frac n2\) [2a + (n − 1)d]
जब a = 1 तथा d = \(\frac 12\)
प्रथम 16 पदों का योग,
S16 = \(\frac {16}2\) [2 × 1 + (16 – 1) × \(\frac 12\) ]
= 8 (2 + 15 × \(\frac 12\))
= 8 × \(\frac {4 + 15}2\)
= 76
जब a = 5 तथा d = \(-\;\frac 12\)
प्रथम 16 पदों का योग,
S16 = \(\frac {16}2\) [2 × 5 + (16 – 1) × \(-\;\frac 12\) ]
= 8 (10 + 15 × \(-\;\frac 12\))
= 8 × \(\frac {20 – 15}2\)
= 20
अत:, प्रथम 16 पदों का योग 76 अथवा 20 है। (उत्तर)
3. एक सीढ़ी के क्रमागत डण्डे परस्पर 25 cm की दूरी पर हैं। (देखिए संलग्न आकृति 5.4) डण्डों की लम्बाई एक समान रूप से घटती जाती है तथा सबसे निचले डण्डे की लम्बाई 45 cm है और सबसे ऊपर वाले डण्डे की लम्बाई 25 cm है। यदि ऊपरी और निचले डण्डे के बीच की दूरी \(2\frac 12\) m है, तो डण्डों को बनाने के लिए लकड़ी की कितनी लम्बाई 25 cm की आवश्यकता होगी?
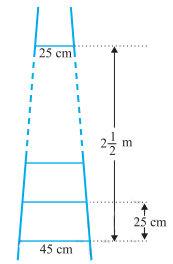
हल:
क्रमागत दो डंडों के बीच की दूरी = 25 cm
ऊपरी और निचले डण्डे के बीच की दूरी = 2.5m = 2.5 × 100 cm = 250 cm
चूँकि डण्डों की संख्या = \(\frac {250}{25}\) + 1 = 11
प्रथम पद, a = 45
अन्तिम पद, l = 25
पदों की संख्या, n = 11
हम जानते हैं कि, प्रथम n पदों का योग,
Sn= \(\frac n2\) (a + l)
S11 = \(\frac {11}2\) (45 + 25)
= \(\frac {11}2\) × 70
= 11 × 35
= 385 cm
अत:, लकड़ी की कुल लम्बाई = 385 cm (उत्तर)
4. एक पंक्ति के मकानों को क्रमागत रूप से 1 से 49 तक अंकित किया गया है। दर्शाइए कि x.का एक ऐसा मान है कि x से अंकित मकान से पहले के मकानों की संख्याओं का योग उसके बाद वाले मकानों की संख्याओं के योग के बराबर है। x का मान ज्ञात कीजिए।
हल:
मकानों के क्रमांक क्रमशः 1, 2, 3, 4,…….49
प्रथम पद, a = 1
सार्व अंतर, d = 1
पदों की संख्या, n = 49
प्रश्नानुसार,
Sx – 1 = S49 – Sx …………………………(i)
हम जानते हैं कि,
प्रथम n पदों का योग, Sn = \(\frac n2\) [2a + (n − 1)d]
Sx = \(\frac x2\) [ 2×1 + (x − 1)1]
⇒ Sx = \(\frac x2\) (2 + x − 1)
⇒ Sx = \(\frac x2\)(x + 1)
⇒ Sx = \(\frac{x^{2}\;+\;x}{2}\) …………………………(ii)
इसी तरह से,
Sx – 1 = \(\frac {x\;-\;1}2\) [ 2×1 + (x − 1 – 1)1]
⇒ Sx – 1 = \(\frac {x\;-\;1}2\) [ 2 + x − 2]
⇒ Sx – 1 = \(\frac {x\;-\;1}2\) × x
⇒ Sx – 1 = \(\frac{x^{2}\;-\;x}{2}\) …………………………(iii)
इसी तरह से,
S49 = \(\frac {49}2\) [ 2×1 + (49 − 1)1]
⇒ S49 = \(\frac {49}2\) (2 + 48)
⇒ S49 = \(\frac {49}2\) × 50
⇒ S49 = 49 × 25
⇒ S49 = 1225 …………………………(iii)
Sx−1, Sx तथा S49 का मान समीकरण (i) में रखने पर,
Sx – 1 = S49 – Sx
⇒ \(\frac{x^{2}\;-\;x}{2}\) = 1225 – \(\frac{x^{2}\;+\;x}{2}\)
⇒ \(\frac{x^{2}\;-\;x}{2}\) + \(\frac{x^{2}\;+\;x}{2}\) = 1225
⇒ \(\frac {x^{2}\;-\;x\;+\;x^{2}\;+\;x}{2}\) = 1225
⇒ \(\frac {2x^{2}}{2}\) = 1225
⇒ x2 = 1225
⇒ x = \(\sqrt{1225}\)
⇒ x = ± 35 [x का मान कभी भी ऋणात्मक नहीं हो सकता है]
अतः, x का मान = 35 (उत्तर)
5. एक फुटबॉल के मैदान में एक छोटा चबूतरा है, जिसमें 15 सीढ़ियाँ बनी हुई हैं। इन सीढ़ियों में से प्रत्येक की लम्बाई 50 m है और वह ठोस कंक्रीट (Concrete) की बनी है। प्रत्येक सीढ़ी में \(\frac 14\) m की चढ़ाई है और \(\frac 12\) m का फैलाव (चौड़ाई) है। (देखिए संलगन आकृति 5.5) इस चबूतरे को बनाने में लगी कुल कंक्रीट का आयतन परिकलित कीजिए।
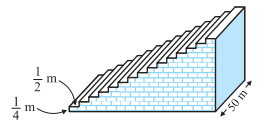
हल:
पहली सीढ़ी का आयतन, a1 = \(\frac{1}{4}\times \frac{1}{2}\times 50\;=\;\frac{1}{4}\times 25\) cm3
दूसरी सीढ़ी का आयतन, a2 = \(\frac{2}{4}\times \frac{1}{2}\times 50\;=\;\frac{2}{4}\times 25\) cm3
तीसरी सीढ़ी का आयतन, a3 = \(\frac{3}{4}\times \frac{1}{2}\times 50\;=\;\frac{3}{4}\times 25\) cm3
……..
अंतिम सीढ़ी का आयतन, a15 = \(\frac{15}{4}\times \frac{1}{2}\times 50\;=\;\frac{15}{4}\times 25\) cm3
सार्व अंतर, d = a2 – a1 = \(\frac{2}{4}\times 25\;-\;\frac{1}{4}\times 25\) = \(\frac{1}{4}\times 25\)
हम जानते हैं कि,
प्रथम n पदों का योग, Sn = \(\frac n2\) [2a + (n − 1)d]
S15 = \(\frac{15}{2} \left [ 2\left ( \frac{1}{4} \times 25\right )\;+\;\left ( 15\;-\;1 \right ) \left ( \frac{1}{4}\times 25 \right )\right ] \)
= \(\frac{15}{2} \left [ \frac{25}{2}\;+\;\frac{175}{2} \right ]\)
= \(\frac{15}{2} \times \frac{200}{2}\)
= 750 m3
अतः, कंक्रीट का आयतन = 750 m3 (उत्तर)
![]()
NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi NCERT Solutions for Class 10 Maths Chapter 5.4 arithmetic arithmetic in hindi