NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi

NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi

एनसीईआरटी कक्षा 10 गणित अध्याय 15 अभ्यास 15.1 प्रायिकता समाधान हिंदी में: क्या आप कक्षा 10 के गणित के एनसीईआरटी समाधान हिंदी में खोज रहे हैं, यदि हाँ तो आप सही जगह पर आए हैं? हमारे विशेषज्ञ ने सभी विषयों के लिए एनसीईआरटी कक्षा 10 के समाधान बहुत ही वर्णनात्मक तरीके से बनाए हैं ताकि कोई भी छात्र इसे आसानी से समझ सके। हिंदी में यह समाधान सभी छात्रों के लिए बहुत मददगार होने वाला है। हमने सभी विषयों के एनसीईआरटी कक्षा 10 के नोट्स भी बहुत ही सरल तरीकों से हिंदी में बनाए हैं।

1. निम्नलिखित कथनों को पूरा कीजिए :

(i) घटना E की प्रायिकता + घटना ‘E नहीं’ की प्रायिकता = ___________  है।

(ii) उस घटना की प्रायिकता जो घटित नहीं हो सकती __________ है। ऐसी घटना ________ कहलाती है।

(iii) उस घटना की प्रायिकता जिसका घटित होना निश्चित है _________ है। ऐसी घटना _________ कहलाती है।

(iv) किसी प्रयोग की सभी प्रारम्भिक घटनाओं का योग __________ है।

(v) किसी घटना की प्रायिकता __________ से बड़ी या उसके बराबर होती है तथा __________ से छोटी या उसके बराबर होती है।

हल :

(i) घटना E की प्रायिकता + घटना ‘E नहीं’ की प्रायिकता = 1 है।

(ii) उस घटना की प्रायिकता जो घटित नहीं हो सकती 0 है। ऐसी घटना असम्भव घटना कहलाती है।

(iii) उस घटना की प्रायिकता जिसका घटित होना निश्चित है 1 है। ऐसी घटना निश्चित घटना कहलाती है।

(iv) किसी प्रयोग की सभी प्रारम्भिक घटनाओं का योग 1 है।

(v) किसी घटना की प्रायिकता 0 से बड़ी या उसके बराबर होती है तथा 1 से छोटी या उसके बराबर होती है।

2. निम्नलिखित प्रयोगों में से किन-किन प्रयोगों के परिणाम समप्रायिक हैं। स्पष्ट कीजिए।

(i) एक ड्राइवर कार चलाने का प्रयत्न करता है। कार चलना प्रारम्भ नहीं होती है।

(ii) एक खिलाड़ी बास्केटबॉल को बास्केट में डालने का प्रयत्न करती है। वह बास्केट में बॉल डाल पाती है या नहीं डाल पाती है।

(iii) एक सत्य-असत्य प्रश्न का अनुमान लगाया जाता है। उत्तर सही है या गलत होगा।

(iv) एक बच्चे का जन्म होता है। वह एक लड़का है या लड़की है।

हल :

(i) परिणाम समप्रायिक नहीं है।

(ii) समप्रायिक नहीं है।

(iii) समप्रायिक है।

(iv) समप्रायिक है।

3. फुटबॉल के खेल को प्रारम्भ करते समय, यह निर्णय लेने के लिए कि कौन-सी टीम पहले बॉल लेगी, इसके लिए सिक्का उछालना एक न्याय संगत विधि क्यों माना जाता है?

हल :

सिक्का उछालना एक न्यायसंगत विधि मानी जाती है क्योंकि जब हम सिक्का उछालते हैं तो चित या पट् आने का परिणाम समसम्भावी है।

4. इनमें से कौन-सी संख्या किसी घटना की प्रायिकता नहीं हो सकती?

(A) \(\frac 23\) (B) -1.5 (C) 15% (D) 0.7

हल :

(B) – 1.5, क्योंकि प्रायिकता कभी ऋणात्मक अर्थात् शून्य से कम नहीं हो सकती है।

5. यदि P(E) = 0.05 है, तो E नहीं की प्रायिकता क्या है?

हल :

हम जानते हैं कि,

P(E) + P(E नहीं) = 1

दिया हुआ है, P(E) = 0.05

∴ P(E नहीं) = 1 – P(E)

या, P(E नहीं) = 1 – 0.05

∴ P(E नहीं) = 0.95 (उत्तर)

6. एक थैले में केवल नीबू की महक वाली गोलियाँ हैं। मालिनी बिना थैले में झाँके उसमें से एक गोली निकालती है। इसकी क्या प्रायिकता है कि वह निकाली गयी गोली
(i) सन्तरे की महक वाली है,
(ii) नीबू की महक वाली है।

हल :

(i) चूंकि थैले में सभी गोलियाँ नींबू की महक वाली हैं।

∴ सन्तरे की महक वाली गोली की संख्या = 0

∴ P(सन्तरे की महक वाली गोली) = \(\frac 01\) = 0 (उत्तर)

(ii) P(नीबू की महक वाली गोली) = 1

7. यह दिया हुआ है कि 3 विद्यार्थियों के एक समूह में से 2 विद्यार्थियों के जन्मदिन एक ही दिन न होने की प्रायिकता 0.992 है। इसकी क्या प्रायिकता है कि इन दो विद्यार्थियों के जन्मदिन एक ही दिन हों?

हल :

2 विद्यार्थियों का एक ही दिन जन्मदिन नहीं होने की घटना की प्रायिकता, P (E नहीं) = 0.992

2 विद्यार्थियों का एक ही दिन जन्मदिन होने की घटना की प्रायिकता, P ( E) = 1 –  P (E नहीं) = 1 –  0.992 = 0.008 (उत्तर)

8. एक थैले में 3 लाल और 5 काली गेंदें हैं। इस थैले में से एक गेंद यादृच्छया निकाली जाती है। इसकी प्रायिकता क्या है कि गेंद
(i) लाल हो?
(ii) लाल नहीं हो?

हल :

थैले में गेंदों की कुल संख्या = लाल गेंदों की संख्या + काली गेंदों की संख्या = 3 + 5 = 8

(i) P(लाल गेंदें) = (लाल गेंदें/कुल गेंदें) = \(\frac 38\) (उत्तर)

(ii) P (लाल गेंदें नहीं) = \(1\;-\;\frac 38 = \frac 58\) (उत्तर)

9. एक डिब्बे में 5 लाल कंचे, 8 सफेद कंचे और 4 हरे कंचे हैं। इस डिब्बे में से एक कंचा यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि निकाला गया कंचा
(i) लाल है?
(ii) सफेद है?
(iii) हरा नहीं है?

हल :

लाल कंचे की संख्या = 5

सफेद कंचे की संख्या = 8

हरे कंचे की संख्या = 4

कुल कंचों की संख्या = 5 + 8 + 4 = 17

(i) P (लाल कंचे) = \(\frac {5}{17}\)

(ii) P (सफेद कंचे) = \(\frac {8}{17}\)

(iii) P (हरे कंचे) = \(\frac {4}{17}\)

∴ P (हरे कंचे नहीं) = 1 – P(हरे कंचे) = 1 – \(\frac {4}{17}\) = \(\frac {13}{17}\) (उत्तर)

10. एक पिग्गी बैंक (Piggy bank) में, 50 पैसे के 100 सिक्के, ₹ 1 के 50 सिक्के, ₹2 के 20 सिक्के और ₹ 5 के 10 सिक्के हैं। यदि पिग्गी बैंक को हिलाकर एक सिक्का गिरने का परिणाम समप्रायिक है, तो इसकी क्या प्रायिकता है कि वह गिरा हुआ सिक्का
(i) 50 पैसे का होना?
(ii) ₹ 5 का नहीं होगा।

हल :

50 पैसे के सिक्कों की संख्या = 100

₹ 1 के सिक्कों की संख्या = 50

₹ 2 के सिक्कों की संख्या = 20

₹ 5 के सिक्कों की संख्या = 10

कुल सिक्कों की संख्या = 100 + 50 + 20 + 10 = 180

(i) P (50 पैसे के सिक्के) = \(\frac {100}{180} = \frac 59\)

(ii) P (₹5 के सिक्के) = \(\frac {10}{180} = \frac {1}{18}\)

∴ P (₹5 के सिक्के नहीं) = 1 – P (₹5 के सिक्के) = 1 – \(\frac {1}{18} = \frac {17}{18}\)

11. गोपी अपने जल-जीव कुण्ड (aquarium) के लिए एक दुकान से मछली खरीदती है। दुकानदार एक टंकी, जिसमें 5 नर मछलियाँ एवं 8 मादा मछलियाँ है, में से एक मछली यादृच्छिक उसे देने के लिए निकालती है (देखिए आकृति 15.4)। इसकी क्या प्रायिकता है कि निकाली गयी मछली नर मछली है।

हल :

नर मछलियों की संख्या = 5

मादा मछलियों की संख्या = 8

कुल मछलियाँ की संख्या = 5 + 8 = 13

P (नर मछली) = \(\frac {5}{13}\)

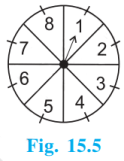
12. संयोग (Chance) के एक खेल में एक तीर घुमाया जाता है जो विश्राम में आने के बाद संख्याओं 1, 2, 3, 4, 5, 6, 7 और 8 में से किसी एक संख्या को इंगित करता है (देखिए आकृति 15.5)। यदि ये सभी परिणाम समप्रायिक हों, तो इसकी क्या प्रायिकता है कि यह तीर इंगित
(i) 8 को करेगा?
(ii) एक विषम संख्या को करेगा?
(iii) 2 से बड़ी संख्या को करेगा?
(iv) 9 से छोटी संख्या को करेगा?

हल :

कुल संख्याएँ = 8

(i) P (8 को तीर इंगित) = \(\frac 18\)

(ii) कुल विषम संख्याएँ = 4

P (एक विषम संख्या) = \(\frac 48 = \frac 12\)

(iii) 2 से बड़ी संख्याएँ = 6

P (2 से बड़ी संख्या) = \(\frac 68 = \frac 34\)

(iv) 9 से छोटी संख्याएँ = 8

P (9 से छोटी संख्या) = \(\frac 88\) = 1

13. एक पासे को एक बार फेंका जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए
(i) एक अभाज्य संख्या।
(ii) 2 और 6 के बीच स्थित कोई संख्या।
(iii) एक विषम संख्या।

हल :

कुल सम्भावित परिणाम = 6

(i) अभाज्य संख्याओं की संख्या = 3 (2, 3 और  5)

P (एक अभाज्य संख्या) = \(\frac 36 = \frac 12\)

(ii) 2 और 6 के बीच संख्याएँ = 3 (3, 4 और  5)

P (2 और 6 के बीच स्थित कोई संख्या) = \(\frac 36 = \frac 12\)

(iii) विषम संख्याएँ हैं  = 3 (1, 3 और  5)

P (एक विषम संख्या) = \(\frac 36 = \frac 12\)

14. 52 पत्तों की अच्छी तरह फेंटी गयी एक गड्डी में से एक पत्ता निकाला जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए
(i) लाल रंग का बादशाह।
(ii) एक फेस कार्ड अर्थात् तस्वीर वाला पत्ता।
(iii) लाल रंग का तस्वीर वाला पत्ता।
(iv) पान का गुलाम।
(v) हुकुम का पत्ता।
(vi) एक ईंट की बेगम।

हल :

तास की एक गड्डी में पत्तों की संख्या = 52

(i) लाल रंग के बादशाहों की संख्या = 2

P (लाल रंग का बादशाह) = \(\frac {2}{52} = \frac {1}{26}\)

(ii) तस्वीर वाला पत्ता की संख्या = 12

P (तस्वीर वाला पत्ता) = \(\frac {12}{52} = \frac {3}{13}\)

(iii) लाल रंग का तस्वीर वाला पत्ता की संख्या = 6

P (लाल रंग का तस्वीर वाला पत्ता) = \(\frac {6}{52} = \frac {3}{26}\)

(iv) पान का गुलाम की संख्या = 1

P (पान का गुलाम) = \(\frac {1}{52}\)

(v) हुकुम का पत्ता की संख्या = 13

P (हुकुम का पत्ता) = \(\frac {13}{52} = \frac 14\)

(vi) एक ईंट की बेगम की संख्या = 1

P (एक ईंट की बेगम) = \(\frac {1}{52}\)

15. ताश के पाँच पत्तों-ईंट का दहला, गुलाम, बेगम, बादशाह और इक्का को पलटकर खूब फेंट दिया जाता है। फिर इनमें से पत्ता यादृच्छया निकाला जाता है।
(i) इसकी क्या प्रायिकता है कि यह एक बेगम है?
(ii) यदि बेगम निकल आती है, तो उसे अलग रख दिया जाता है और एक अन्य पत्ता निकाला जाता है। इसकी क्या प्रायिकता है कि दूसरा निकाला गया पत्ता (a) एक इक्का है? (b) एक बेगम है?

हल :

कुल पत्ते की संख्या = 5

(i) बेगम के पत्ते की संख्या = 1

P (एक बेगम का पत्ता) = \(\frac 15\)

(ii) बेगम के पत्ते को निकालकर एक ओर रखने पर, पत्ते की संख्या (5 – 1) = 4

(a) इक्का के पत्ते की संख्या = 1

P (एक इक्का का पत्ता) = \(\frac 14\)

(b) बेगम के पत्ते की संख्या = 0

P (एक बेगम का पत्ता) = \(\frac 04\) = 0

16. किसी कारण 12 खराब पेन 132 अच्छे पेनों में मिलाए गए हैं। केवल देखकर यह नहीं बताया जा सकता कि कोई पेन खराब है या अच्छा है। इस मिश्रण में से एक पेन यादृच्छया निकाला जाता है। निकाले गए पेन की अच्छा होने की प्रायिकता ज्ञात कीजिए।

हल :

खराब पेनों की संख्या = 12

अच्छे पेनों की संख्या = 132

कुल पेन = 12 + 132 = 144

P(अच्छे पेन) = \(\frac {132}{144} = \frac {11}{12}\)

17. (i) 20 बल्बों के एक समूह में 4 बल्ब खराब हैं। इस समूह में से एक बल्ब यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि बल्ब खराब होगा?

(ii) (ii) मान लीजिए (i) में निकाला गया बल्ब खराब नहीं है और न ही इसे दुबारा बल्बों के साथ मिलाया जाता है। अब शेष बल्बों में से एक बल्ब यादृच्छया निकाला जाता है। इसकी क्या प्रायकिता है कि यह बल्ब खराब नहीं होगा?

हल :

कुल बल्बों की संख्या = 20

(i) खराब बल्बों की संख्या = 4

P (खराब बल्ब) = \(\frac {4}{20} = \frac 15\)

(ii)  कुल बल्बों की संख्या = 20 – 1 = 19

शेष बचे बल्बों में अच्छे बल्बों की संख्या = 19 – 4 = 15

P(बल्ब खराब नहीं) = \(\frac {15}{19}\)

18. एक पेटी में 90 डिस्क (discs) हैं, जिन पर 1 से 9 संख्याएँ अंकित हैं। यदि इस पेटी में से एक डिस्क यादृच्छया निकाली जाती है, तो इसकी प्रायिकता ज्ञात कीजिए कि इस डिस्क पर अंकित होगी,
(i) दो अंकों की संख्या,
(ii) एक पूर्ण वर्ग संख्या,
(iii) 5 से विभाज्य एक संख्या?

हल :

पेटी में डिस्कों की संख्या = 90

(i) दो अंकों वाली कुल संख्याएँ = 81

P (दो अंकों की संख्या) = \(\frac {81}{90} = \frac {9}{10}\)

(ii) पूर्ण वर्ग की कुल संख्याएँ = 9 (1, 4, 9, 16, 25, 36, 49, 64 तथा 81)

P (एक पूर्ण वर्ग संख्या) = \(\frac {9}{90} = \frac {1}{10}\)

(iii) 5 से विभाज्य कुल संख्याएँ = 18 (5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85 तथा 90)

P (5 से विभाज्य एक संख्या) = \(\frac {18}{90} = \frac 15\)

19. एक बच्चे के पास ऐसा पासा है, जिसके फलकों पर निम्नलिखित अक्षर अंकित हैं

इस पासे को एक बार फेंका जाता है। इसकी क्या प्रायिकता है कि
(i) A प्राप्त हो?
(ii) D प्राप्त हो?

हल :

सम्भव परिणामों की कुल संख्या = 6

(i) अक्षर A  = 2

P (A प्राप्त हो) = \(\frac 26 = \frac 13\)

(ii) अक्षर D  = 1

P (D प्राप्त हो) = \(\frac 16\)

20. मान लीजिए आप एक पासे को आकृति 15.6 में दर्शाए गए आयताकार क्षेत्र में यादृच्छया रूप से गिराते हैं। इसकी क्या प्रायिकता है कि वह पासा 1 m व्यास वाले वृत्त के अन्दर गिरेगा?

हल :

आयत का क्षेत्रफल = l ✕ b = 3 ✕ 2 = 6 m²

वृत्त का क्षेत्रफल =  πr² = \(\pi\left ( \frac{1}{2} \right )^{2} = \frac{\pi}{4}\) m²

P(पासा 1 m व्यास वाले वृत्त के अन्दर गिरेगा) = \(\frac{\frac{\pi}{4}}{6} = \frac{\pi}{24}\)

21. 144 बॉल पेनों के समूह में 20 बॉल पेन खराब हैं और शेष अच्छे हैं। आप वही पेन खरीदना चाहेंगे, जो अच्छा हो, परन्तु खराब पेन आप खरीदना नहीं चाहेंगे। दुकानदार इन पेनों में से, यादृच्छया एक पेन निकालकर आपको देता है। इसकी क्या प्रायिकता है कि
(i) आप पेन खरीदेंगे?
(ii) आप पेन नहीं खरीदेंगे?

हल :

पेनों की कुल संख्या = 144

खराब पेनों की संख्या = 20

अच्छे पेनों की संख्या = 144 – 20 = 124

(i) P( आप पेन खरीदेंगे) = \(\frac {124}{144} = \frac {31}{36}\)

(ii) P(आप पेन नहीं खरीदेंगे) = \(\frac {20}{144} = \frac {5}{36}\)

22. उदाहरण 13 को देखिए (i) निम्नलिखित सारणी को पूरा कीजिए :

घटना : दोनों पासों की संख्याओं का योग	2	3	4	5	6	7	8	9	10	11	12
प्रायिकता	\(\frac {1}{36}\)						\(\frac {5}{36}\)				\(\frac {1}{36}\)

(ii) एक विद्यार्थी यह तर्क देता है कि यहाँ कुल 11 परिणाम 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 एवं 12 हैं। अतः प्रत्येक की प्रायिकता \(\frac {1}{11}\) है। क्या आप इस तर्क से सहमत हैं ? सकारण उत्तर दीजिए।

हल :

(i) सम्भव परिणामों की कुल संख्या = 6 × 6 = 36

दोनों पासों की संख्याओं का योग 3 के अनुकूल परिणामों की संख्या = 2 (1,2)  तथा (2,1)

P(योग 3) = \(\frac {2}{36}\)

दोनों पासों की संख्याओं का योग 4 के अनुकूल परिणामों की संख्या = 3 (1,3), (3,1),  तथा (2,2)

P(योग 4) = \(\frac {3}{36}\)

दोनों पासों की संख्याओं का योग 5 के अनुकूल परिणामों की संख्या = 4 (1,4), (4,1), (2,3),  तथा (3,2)

P(योग 5) = \(\frac {4}{36}\)

दोनों पासों की संख्याओं का योग 6 के अनुकूल परिणामों की संख्या = 5 (1,5), (5,1), (2,4), (4,2),  तथा (3,3)

P(योग 6) = \(\frac {5}{36}\)

दोनों पासों की संख्याओं का योग 7 के अनुकूल परिणामों की संख्या = 6 (1,6), (6,1), (5,2), (2,5), (4,3),  तथा (3,4)

P(योग 7) = \(\frac {6}{36}\)

दोनों पासों की संख्याओं का योग 9 के अनुकूल परिणामों की संख्या = 4 (3,6), (6,3), (4,5),  तथा (5,4)

P(योग 9) = \(\frac {4}{36}\)

दोनों पासों की संख्याओं का योग 10 के अनुकूल परिणामों की संख्या = 3 (4,6), (6,4),  तथा (5,5)

P(योग 10) = \(\frac {3}{36}\)

दोनों पासों की संख्याओं का योग 11 के अनुकूल परिणामों की संख्या = 2 (5,6),  तथा (6,5)

P(योग 11) = \(\frac {2}{36}\)

घटना : दोनों पासों की संख्याओं का योग	2	3	4	5	6	7	8	9	10	11	12
प्रायिकता	\(\frac {1}{36}\)	\(\frac {2}{36}\)	\(\frac {3}{36}\)	\(\frac {4}{36}\)	\(\frac {5}{36}\)	\(\frac {6}{36}\)	\(\frac {5}{36}\)	\(\frac {4}{36}\)	\(\frac {3}{36}\)	\(\frac {2}{36}\)	\(\frac {1}{36}\)

(ii) यह तर्क सही नहीं है, क्योंकि सभी संभव परिणामों की संख्या 36 है, 11 नहीं।

23. एक खेल में एक रुपए के सिक्के को तीन बार उछाला जाता है और प्रत्येक बार का परिणाम लिख लिया जाता है। तीनों परिणाम समान होने पर अर्थात् तीन चित या तीन पट प्राप्त होने पर हनीफ खेल जीत जायेगा, अन्यथा हार जायेगा। हनीफ के खेल में हार जाने की प्रायिकता परिकल्पित कीजिए।

हल :

कुल संभावित परिणाम की संख्या = 8 (HHH, HHT, HTH, THH, TTH, HTT, THT, TTT)

हनीफ के खेल में हारने का अनुकूल  परिणाम = 6

P (हनीफ के खेल में हारने की प्रायिकता) = \(\frac 68 = \frac 34\)

24. एक पासे को दो बार फेंका जाता है। इसकी प्रायिकता क्या है कि
(i) 5 किसी भी बार नहीं आयेगा?
(ii) 5 कम से कम एक बार आयेगा?

हल :

(i) सम्भव परिणामों की कुल संख्या = 6 × 6 = 36

5 एक भी बार न आने की घटना = 25

5 एक भी बार आने की घटना = 36 – 25 = 11

P(5 किसी भी बार नहीं आयेगा) = \(\frac {25}{36}\)

(ii) P(5 कम से कम एक बार आयेगा) = \(\frac {11}{36}\)

25. निम्नलिखित में से कौन-से तर्क सत्य हैं और कौन-से तर्क असत्य हैं? सकारण उत्तर दीजिए।
(i) यदि दो सिक्कों को एक साथ उछाला जाता है, तो इसके तीन सम्भावित परिणाम दो चित, दो पट या प्रत्येक एक बार है। अतः इनमें से प्रत्येक परिणाम की प्रायिकता \(\frac 13\) है।
(ii) यदि एक पासे को फेंका जाता है, तो इसके दो सम्भावित परिणाम एक विषम संख्या या एक सम संख्या है। अत: एक विषम संख्या ज्ञात करने की प्रायिकता \(\frac 12\) है।

हल :

(i) सम्भव परिणामों की कुल संख्या { (H,H); (H,T); (T,H) तथा (T,T)} = 4

P (दो चित) = \(\frac 14\)

P (दो पट) = \(\frac 14\)

P (प्रत्येक एक बार) =\(\frac 24 = \frac 12\)

∴ यह कथन सत्य नहीं है।

(ii) सम्भव परिणामों की कुल संख्या (1, 2, 3, 4, 5, 6) = 6

P(एक विषम संख्या) = \(\frac 36 = \frac 12\)

P(एक सम संख्या) = \(\frac 36 = \frac 12\)

हाँ, यह कथन सत्य है।

NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi

NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi NCERT Solutions for Class 10 Maths Chapter 15 Probability in hindiNCERT Solutions for Class 10 Maths Chapter 15 Probability in hindiNCERT Solutions for Class 10 Maths Chapter 15 Probability in hindi