NCERT Solutions for Class 10 Maths Chapter 14.3 statistics in hindi
एनसीईआरटी कक्षा 10 गणित अध्याय 14: सांख्यिकी प्रश्नावली 14.3 समाधान हिंदी में: क्या आप कक्षा 10 के गणित के एनसीईआरटी समाधान हिंदी में खोज रहे हैं, यदि हाँ तो आप सही जगह पर आए हैं? हमारे विशेषज्ञ ने सभी विषयों के लिए एनसीईआरटी कक्षा 10 के समाधान बहुत ही वर्णनात्मक तरीके से बनाए हैं ताकि कोई भी छात्र इसे आसानी से समझ सके। हिंदी में यह समाधान सभी छात्रों के लिए बहुत मददगार होने वाला है। हमने सभी विषयों के एनसीईआरटी कक्षा 10 के नोट्स भी बहुत ही सरल तरीकों से हिंदी में बनाए हैं।
![]()
अध्याय 14: सांख्यिकी प्रश्नावली 14.3
1. निम्नलिखित बारंबारता बंटन किसी मोहल्ले के 68 उपभोक्ताओं की बिजली की मासिक खपत दर्शाता है। इन आँकड़ों के माध्यक, माध्य और बहुलक ज्ञात कीजिए। इनकी तुलना कीजिए।
| मासिक खपत (इकाईयों में) | उपभोक्ताओं की संख्या |
| 65-85 | 4 |
| 85-105 | 5 |
| 105-125 | 13 |
| 125-145 | 20 |
| 145-165 | 14 |
| 165-185 | 8 |
| 185-205 | 4 |
हल :
माध्यक के लिए :
| मासिक खपत (इकाईयों में) | उपभोक्ताओं की संख्या (f) | संचयी बारंबारता (cf) |
| 65-85 | 4 | 4 |
| 85-105 | 5 | 9 |
| 105-125 | 13 | 22 |
| 125-145 | 20 | 42 |
| 145-165 | 14 | 56 |
| 165-185 | 8 | 64 |
| 185-205 | 4 | 68 |
| n = 68 |
∵ n = 68
∴ \(\frac n2 = \frac {68}{2}\) = 34
यहां, माध्यक वर्ग = 125 – 145, l = 125, cf = 22, f = 20, h = 20
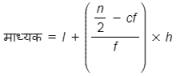
= \(125\;+\;\left ( \frac{34\;-\;22}{20} \right )\;\times 20\)
= 125 + 12
= 137 (उत्तर)
बहुलक के लिए :
बहुलक वर्ग = 125 – 145
निम्न सीमा, l = 125,
बारंबारता, f1 = 20,
इससे पहले वर्ग की बारंबारता, f0 = 13,
इससे ठीक बाद के वर्ग की बारंबारता, f2 = 14,
वर्ग माप, h = 20
![]()
= \(125\;+\;\frac{20\;-\:13}{40\;-\;13\;-\;14}\;\times 20\)
= \(125\;+\;\frac{7\;\times 20}{13}\)
= 125 + 10.76
= 135.76 (उत्तर)
माध्य के लिए :
![]()
कल्पित माध्य, a = 135, वर्गमाप, h = 20
| मासिक खपत (इकाईयों में) | उपभोक्तओं की संख्या (fi) | वर्ग चिह्न (xi) | di= xi – a | \(u_{i} = \frac{d_{i}}{h}\) | fiui |
| 65-85 | 4 | 75 | -60 | -3 | -12 |
| 85-105 | 5 | 95 | -40 | -2 | -10 |
| 105-125 | 13 | 115 | -20 | -1 | -13 |
| 125-145 | 20 | 135 | 0 | 0 | 0 |
| 145-165 | 14 | 155 | 20 | 1 | 14 |
| 165-185 | 8 | 175 | 40 | 2 | 16 |
| 185-205 | 4 | 195 | 60 | 3 | 12 |
| योग | ∑ fi= 68 | ∑ fiui= 7 |
![]()
= \(135\;+\;20\left (\frac{7}{68} \right )\)
= 135 + 2.06
= 137.06 (उत्तर)
अतः, इन आँकड़ों के माध्यक, माध्य और बहुलक बराबर हैं।
2. यदि नीचे दिए हुए बंटन का माध्यक 28.5 हो, तो x और y के मान ज्ञात कीजिए :
| वर्ग अंतराल | बारंबारता |
| 0-10 | 5 |
| 10-20 | x |
| 20-30 | 20 |
| 30-40 | 15 |
| 40-50 | y |
| 50-60 | 5 |
| योग | 60 |
हल :
| वर्ग अंतराल | बारंबारता (f) | संचयी बारंबारता (cf) |
| 0-10 | 5 | 5 |
| 10-20 | x | 5 + x |
| 20-30 | 20 | 25 + x |
| 30-40 | 15 | 40 + x |
| 40-50 | y | 40 + x + y |
| 50-60 | 5 | 45 + x + y |
| योग | 60 |
दिया है, n = 60
चूँकि, 45 + x + y = 60
x + y = 15 ————(i)
माध्यक = 28.5
\(\frac n2\) = 30
माध्यक वर्ग = 20 – 30
निम्न सीमा, l = 20,
Cf = 5 + x
f = 20 & h = 10
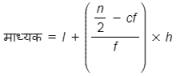
⇒ 28.5 = \(20\;+\;\left ( \frac{30\;-\;(5 + x)}{20} \right )\;\times 10\)
⇒ 28 .5 – 20 = \( \frac {25\;-\;x}{2}\)
⇒ 17 = 25 – x
⇒ x = 25 – 17
⇒ x = 8
अब, x का मान समीकरण (i) में रखने पर,
8 + y = 15
⇒ y = 15 – 8
⇒ y = 7
अतः x = 8 एवं y = 7 हैं। (उत्तर)
3. एक जीवन बीमा एजेण्ट 100 पॉलिसीधारकों की आयु के बण्टन के निम्नलिखित आँकड़े ज्ञात करता है। माध्यक आयु परिकलित कीजिए, यदि पॉलिसी केवल उन्हीं व्यक्तियों को दी जाती है जिनकी आयु 18 वर्ष उससे अधिक हो, परन्तु 60 वर्ष से कम हो।
| आयु (वर्षों में) | पॉलिसीधारकों की संख्या |
| 20 से कम | 2 |
| 25 से कम | 6 |
| 30 से कम | 24 |
| 35 से कम | 45 |
| 40 से कम | 78 |
| 45 से कम | 89 |
| 50 से कम | 92 |
| 55 से कम | 98 |
| 60 से कम | 100 |
हल :
| वर्ग अंतराल | बारंबारता (f) | संचयी बारंबारता (cf) |
| 15-20 | 2 | 2 |
| 20-25 | 4 | 6 |
| 25-30 | 18 | 24 |
| 30-35 | 21 | 45 |
| 35-40 | 33 | 78 |
| 40-45 | 11 | 89 |
| 45-50 | 3 | 92 |
| 50-55 | 6 | 98 |
| 55-60 | 2 | 100 |
दिया है, n = 100
∴ \(\frac n2 = \frac {100}{2}\) = 50
यहां, माध्यक वर्ग = 35 – 40, l = 35, cf = 45, f = 33, h = 5
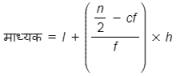
= \(35\;+\;\left ( \frac{50\;-\;45}{33} \right )\;\times 5\)
= 35 + \(\frac {25}{33}\)
= 35 + 0.76
= 35.76 वर्ष (उत्तर)
4. एक पौधे की 40 पत्तियों की लम्बाइयाँ निकटतम मिलीमीटरों में मापी जाती हैं तथा प्राप्त आँकड़ों को निम्नलिखित सारणी के रूप में निरूपित किया जाता है :
| लम्बाई (mm में) | पत्तियों की संख्या |
| 118-126 | 3 |
| 127-135 | 5 |
| 136-144 | 9 |
| 145-153 | 12 |
| 154-162 | 5 |
| 163-171 | 4 |
| 172-180 | 2 |
पत्तियों की माध्यक लम्बाई ज्ञात कीजिए।
हल :
सारणी को सतत वर्ग अन्तराल वाली सारणी में बदलने के लिए ऊपरी सीमा में 0.5 जोड़ देते हैं तथा निम्न सीमा से 0.5 घटा देते हैं।
| लम्बाई (mm में) | पत्तियों की संख्या (f) | संचयी बारंबारता (cf) |
| 117.5-126.5 | 3 | 3 |
| 126.5-135.5 | 5 | 8 |
| 135.5-144.5 | 9 | 17 |
| 144.5-153.5 | 12 | 29 |
| 153.5-162.5 | 5 | 34 |
| 162.5-171.5 | 4 | 38 |
| 171.5-180.5 | 2 | 40 |
∵ n = 40
∴ \(\frac n2 = \frac {40}{2}\) = 20
यहां, माध्यक वर्ग = 144.5 – 153.5, l = 144.5, cf = 17, f = 12, h = 9
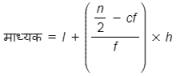
= \(144.5\;+\;\left ( \frac{20\;-\;17}{12} \right )\;\times 9\)
= 144.5 + \(\frac 94\)
= 144.5 + 2.25
= 146.75 mm
अतः, पत्तियों की माध्यक लम्बाई = 146.75 mm. (उत्तर)
5. निम्नलिखित सारणी 400 नियॉन लैंपों के जीवन कालों (life time) को प्रदर्शित करती है:
| जीवन काल (घंटों में) | लैंपों की संख्या |
| 1500-2000 | 14 |
| 2000-2500 | 56 |
| 2500-3000 | 60 |
| 3000-3500 | 86 |
| 3500-4000 | 74 |
| 4000-4500 | 62 |
| 4500-5000 | 48 |
एक लैंप का माध्यक जीवनकाल ज्ञात कीजिए।
हल :
| जीवन काल (घंटों में) | लैंपों की संख्या (f) | संचयी बारंबारता (cf) |
| 1500-2000 | 14 | 14 |
| 2000-2500 | 56 | 70 |
| 2500-3000 | 60 | 130 |
| 3000-3500 | 86 | 216 |
| 3500-4000 | 74 | 290 |
| 4000-4500 | 62 | 352 |
| 4500-5000 | 48 | 400 |
दिया है, n = 400
∴ \(\frac n2 = \frac {400}{2}\) = 200
यहां, माध्यक वर्ग = 3000 – 3500, l = 3000, cf = 130, f = 86, h = 500
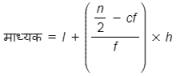
= \(3000\;+\;\left ( \frac{2000\;-\;130}{86} \right )\;\times 500\)
= 3000 + \(\frac {35000}{86}\)
= 3000 + 406.98
= 3406.98
अतः, एक लैंप का माध्यक जीवनकाल = 3406.98 घण्टे (उत्तर)
6. एक स्थानीय टेलीफोन निर्देशिका से 100 कुलनाम (surnames) लिए गए और उनमें प्रयुक्त अंग्रेजी वर्णमाला के अक्षरों की संख्या का निम्नलिखित बारम्बारता बंटन प्राप्त हुआ :
| अक्षरों की संख्या | 1-4 | 4-7 | 7-10 | 10-13 | 13-16 | 16-19 |
| कुलनामों की संख्या | 6 | 30 | 40 | 16 | 4 | 4 |
कुलनामों में माध्यक अक्षरों की संख्या ज्ञात कीजिए। कुलनामों में माध्य अक्षरों की संख्या ज्ञात कीजिए। साथ ही, कुलनामों का बहुलक ज्ञात कीजिए।
हल :
माध्यक के लिए :
| अक्षरों की संख्या | कुलनामों की संख्या (f) | संचयी बारंबारता (cf) |
| 1-4 | 6 | 6 |
| 4-7 | 30 | 36 |
| 7-10 | 40 | 76 |
| 10-13 | 16 | 92 |
| 13-16 | 4 | 96 |
| 16-19 | 4 | 100 |
दिया है, n = 100
∴ \(\frac n2 = \frac {100}{2}\) = 50
यहां, माध्यक वर्ग = 7 – 10, l = 7, cf = 36, f = 40, h = 3
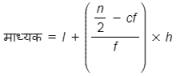
= \(7\;+\;\left ( \frac{50\;-\;36}{40} \right )\;\times 3\)
= 7 + \(\frac {21}{20}\)
= 7 + 1.05
= 8.05 (उत्तर)
बहुलक के लिए :
बहुलक वर्ग = 7 – 10
निम्न सीमा, l = 7,
बारंबारता, f1 = 40,
इससे पहले वर्ग की बारंबारता, f0 = 30,
इससे ठीक बाद के वर्ग की बारंबारता, f2 = 16,
वर्ग माप, h = 3
![]()
= \(7\;+\;\frac{40\;-\:30}{80\;-\;30\;-\;16}\;\times 3\)
= \(7\;+\;\frac{10\;\times 3}{34}\)
= 7 + 0.88
= 7.88 (उत्तर)
माध्य के लिए :
| वर्ग अंतराल | fi | xi | fixi |
| 1-4 | 6 | 2.5 | 15 |
| 4-7 | 30 | 5.5 | 165 |
| 7-10 | 40 | 8.5 | 340 |
| 10-13 | 16 | 11.5 | 184 |
| 13-16 | 4 | 14.5 | 58 |
| 16-19 | 4 | 17.5 | 70 |
| योग | ∑ fi = 100 | ∑ fixi = 832 |
![]()
= \(\frac {832}{100}\)
= 8.32 (उत्तर)
7. नीचे दिया हुआ बंटन एक कक्षा के 30 विद्यार्थियों के भार दर्शा रहा है। विद्यार्थियों का माध्यक ज्ञात कीजिए।
| भार (किग्रा में) | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 |
| विद्यार्थियों की संख्या | 2 | 3 | 8 | 6 | 6 | 3 | 2 |
हल :
| भार (किग्रा में) | विद्यार्थियों की संख्या (f) | संचयी बारंबारता |
| 40-45 | 2 | 2 |
| 45-50 | 3 | 5 |
| 50-55 | 8 | 13 |
| 55-60 | 6 | 19 |
| 60-65 | 6 | 25 |
| 65-70 | 3 | 28 |
| 70-75 | 2 | 30 |
दिया है, n = 30
∴ \(\frac n2 = \frac {30}{2}\) = 15
यहां, माध्यक वर्ग = 55 – 60, l = 55, cf = 13, f =6, h = 5
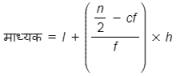
= \(55\;+\;\left ( \frac{15\;-\;13}{6} \right )\;\times 5\)
= 55 + \(\frac 53\)
= 5 + 1.67
= 56.67
अतः, विद्यार्थियों का माध्यक = 56.67 kg. (उत्तर)